task2/PROTOCOL.md

Protocol

In this task, we were supposed to implement two optimization algorithms in an effort to find the minimum value of the functions that we've worked with in the last task. The two algorithms were Local Search (LS) and Stochastic Hill Climbing (SHC). Both of these are pretty similar, the only difference between them is that the LS algorithm includes the center point when determining the minimum, while the SHC algorithm only considers the new points.

From my testing, the SHC algorithm usually performed worse with the same amount of iterations, because LS was more focused on exploring the lowest point of the minimum, while SHC often didn't and instead jumped elsewhere.

That said, because of this fact, SHC actually performed better in cases where LS got stuck in a local minimum, as LS can't recover from this, while SHC can.

Output (graphs)

Below are a few examples of the runs I performed:

Sphere

I first ran the algorithm on the sphere function, with the following settings:

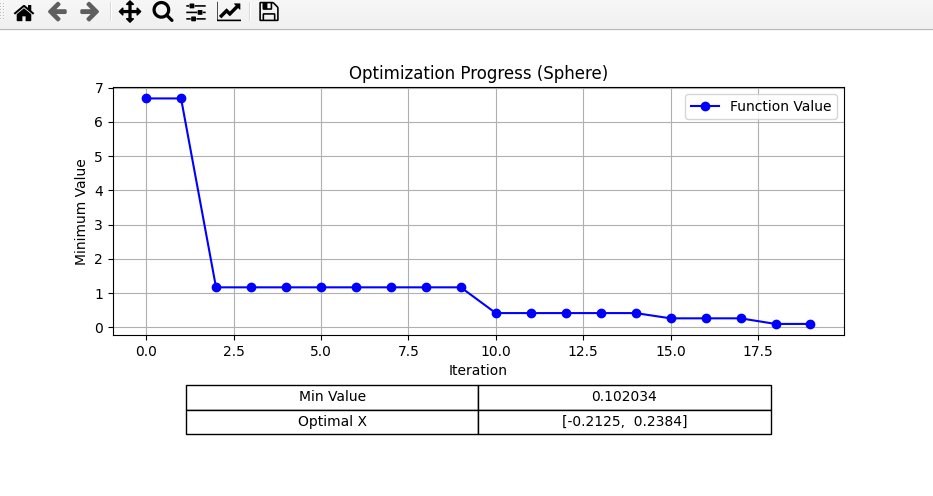
For Local Search, this was the resulting graph:

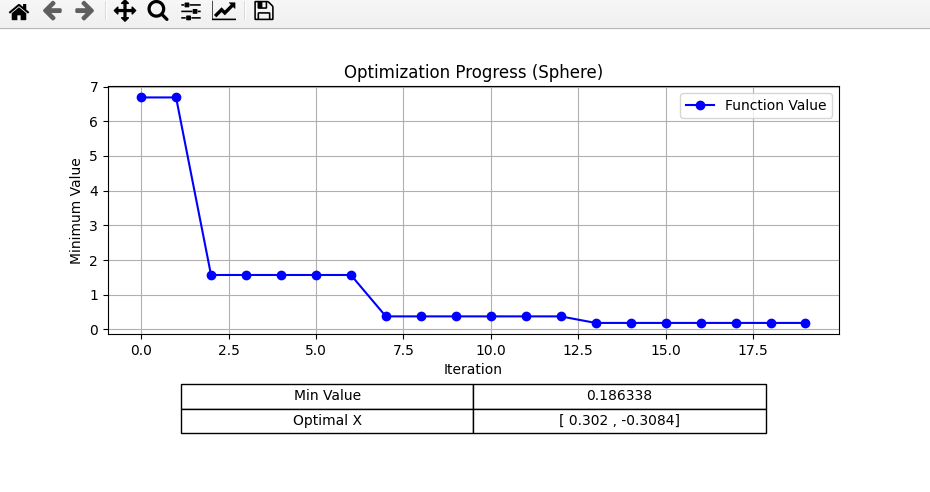
For Stochastic Hill Climbing, the result was this graph:

Rosenbrock

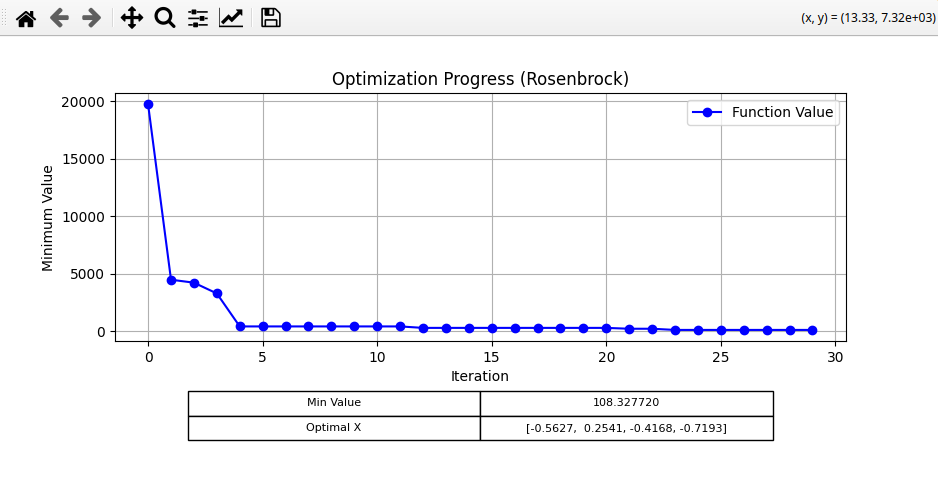
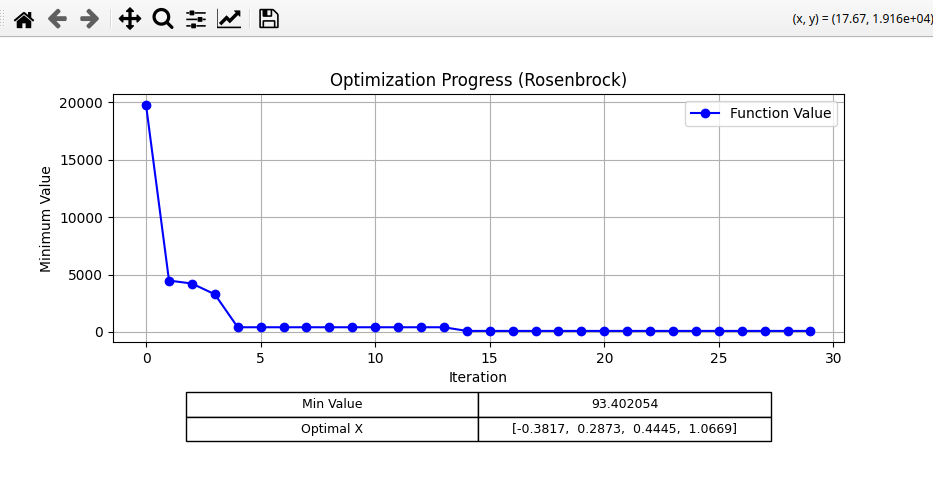
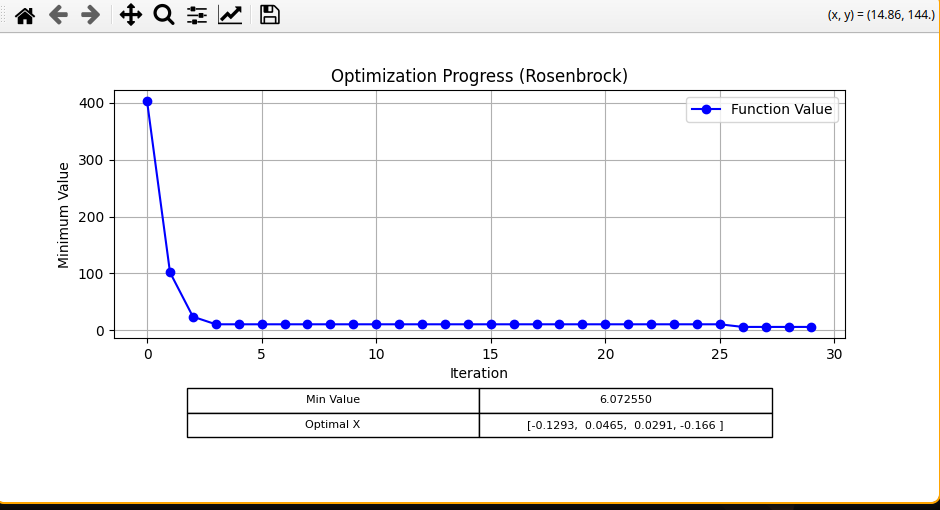
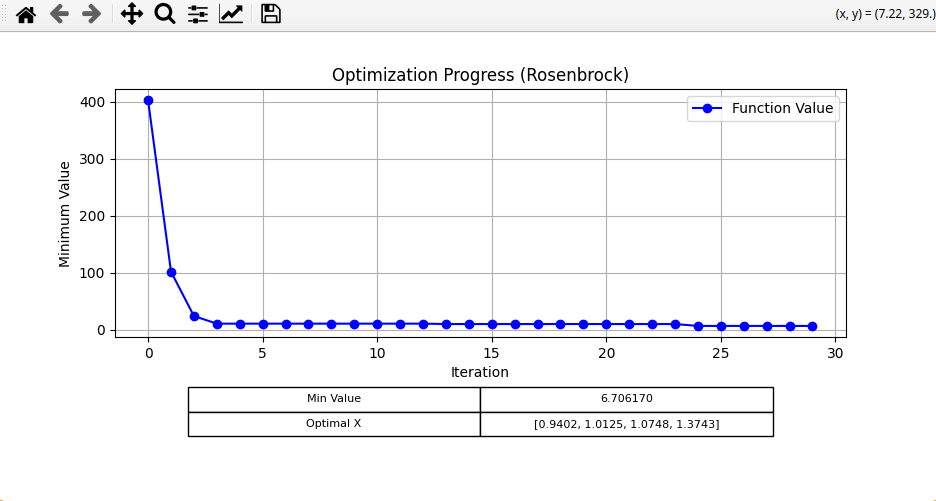
Next, I tried the Rosenbrock function, with the following settings:

For LS, I got:

For SHC, I got:

Further experimenting with Rosenbrock

I also tried adjusting some of the settings with the Rosenbrock function, to compare how they affect the LS and SHC algorithms. Each time, I only modified a single settings, with the rest matching the original Rosenbrock configuration (already shown above).

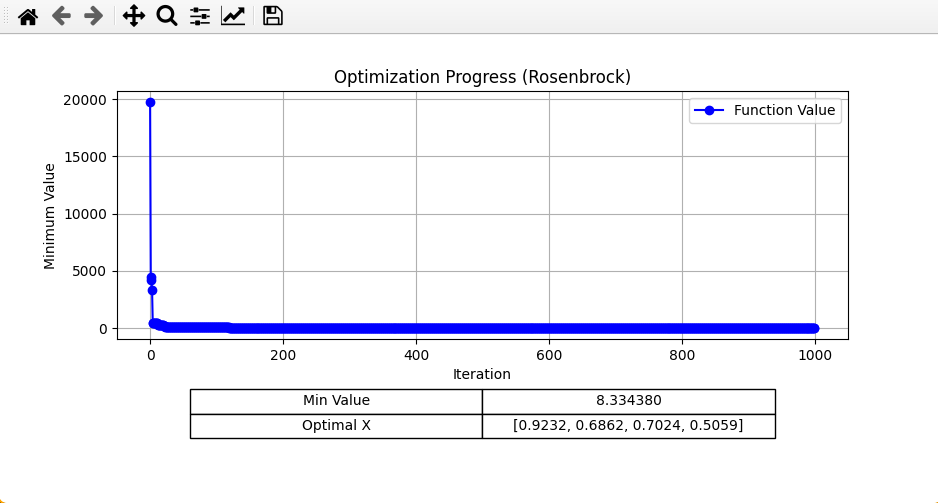
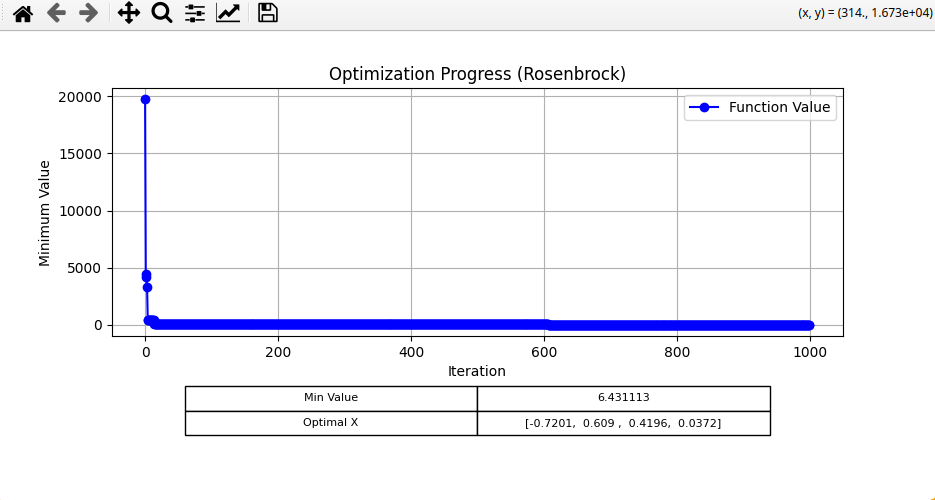
1000 iterations

I first tried increasing the number of iterations to 1000 (from 30).

For LS, I got:

for SHC, I got:

100 neighbors

I then tried increasing the amount of neighbor points to 100 (from 3).

For LS, I got:

for SHC, I got:

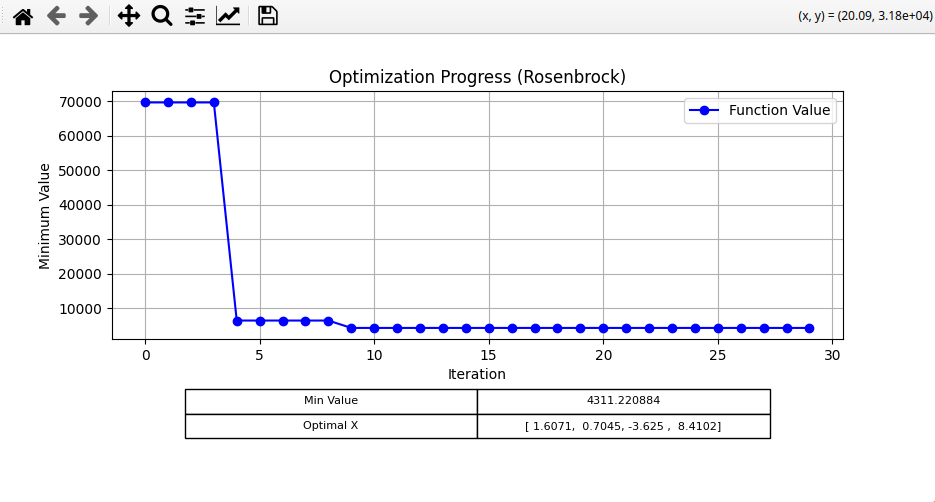
Standard deviation of 30

Finally, I tried increasing the standard deviation of the normal distribution to 30 (from 1.5).

For LS, I got:

for SHC, I got:

Summary

I've tested a bunch more cases locally, however, I didn't want to clutter this report with a bunch of those images, however, from this testing, I found out that in most cases:

• The standard deviation should generally be fairly small, enough to allow precise searching around the minimum however, not too small that the algorithm cannot explore enough of the search space in a single iteration. It's necessary to find a number that balances this and works well.
• The number of iterations only matters up to a certain point. For LS, once a point close to a local minimum is found, additional iterations may only refine the solution slightly, as the probability of finding a better point gets progressively smaller. For SHC, increasing iterations generally improves the chances of escaping local minima and potentially finding a better solution, especially when the standard deviation allows for exploration.
• The number of neighbors is a key factor in performance. Generally, increasing the number of neighbors allows the algorithm to explore more options and find the optimal point faster. However, there are diminishing returns beyond a certain point, where adding more neighbors increases computational cost without improving performance significantly, especially with a small standard deviation.