2.7 KiB
Protocol
In this task, we were supposed to implement two optimization algorithms in an effort to find the minimum value of the functions that we've worked with in the last task. The two algorithms were Local Search (LS) and Stochastic Hill Climbing (SHC). Both of these are pretty similar, the only difference between them is that the LS algorithm includes the center point when determining the minimum, while the SHC algorithm only considers the new points.
From my testing, the SHC algorithm usually performed worse with the same amount of iterations, because LS was more focused on exploring the lowest point of the minimum, while SHC often didn't and instead jumped elsewhere.
That said, because of this fact, SHC actually performed better in cases where LS got stuck in a local minimum, as LS can't recover from this, while SHC can.
Output (graphs)
Below are a few examples of the runs I performed:
Sphere
I first ran the algorithm on the sphere function, with the following settings:
For Local Search, this was the resulting graph:
For Stochastic Hill Climbing, the result was this graph:
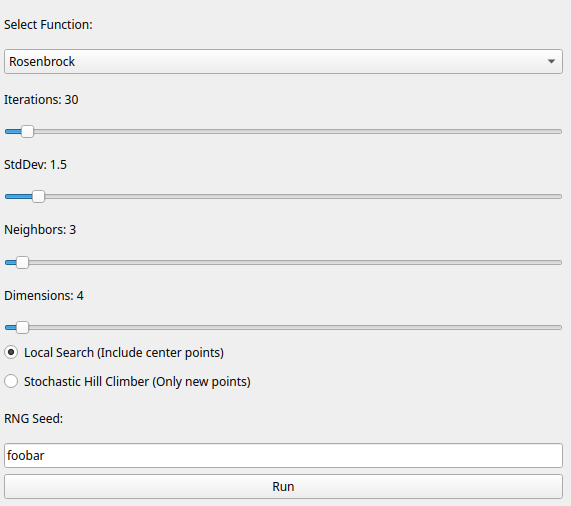
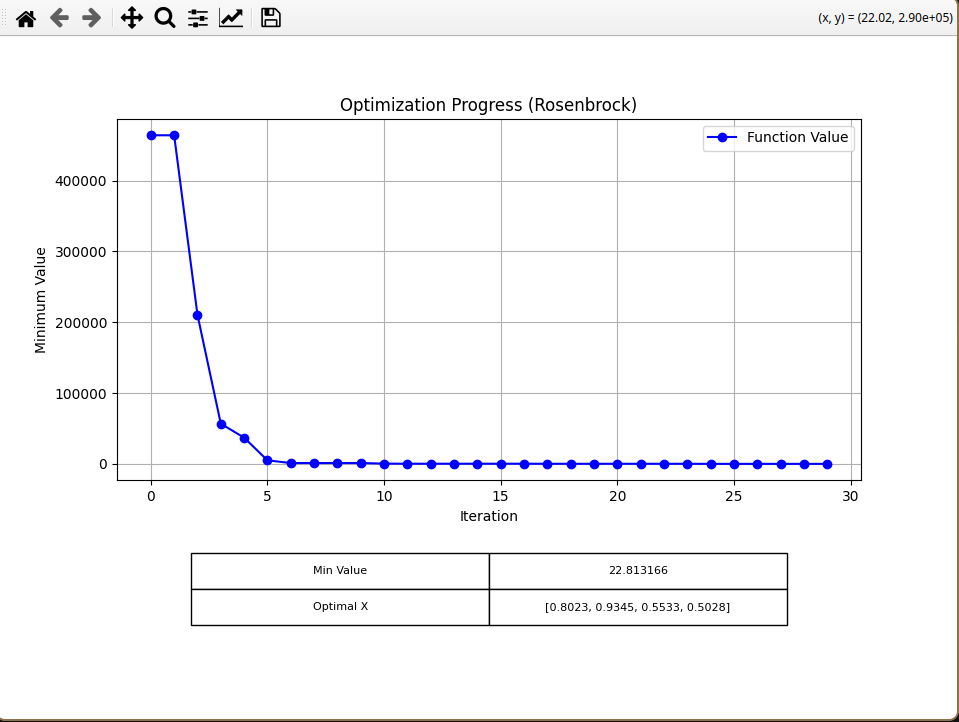
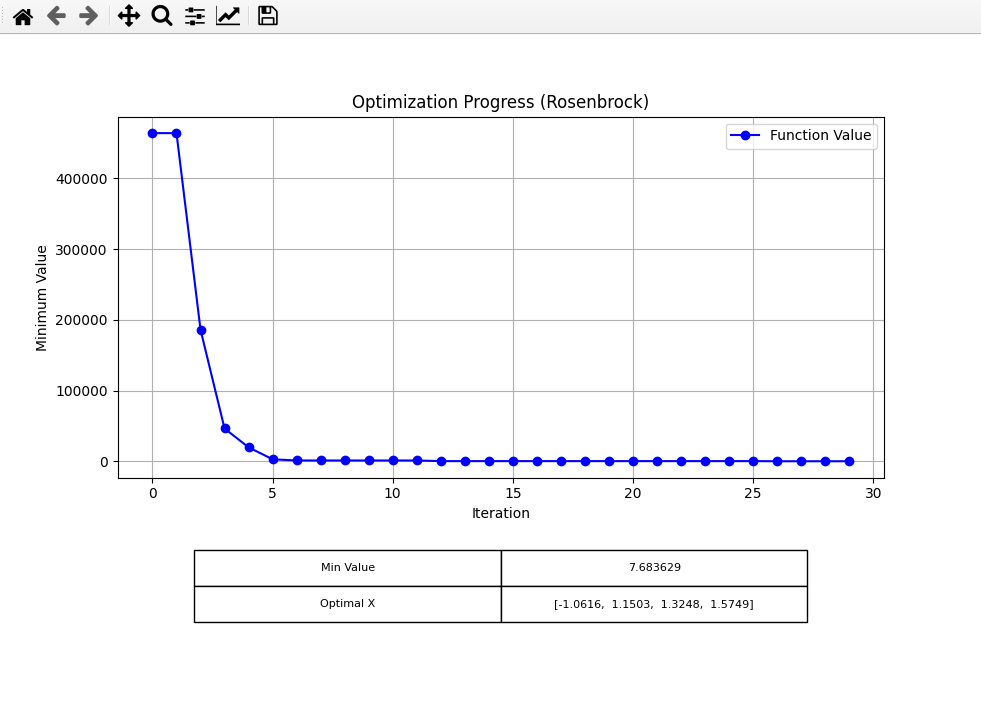
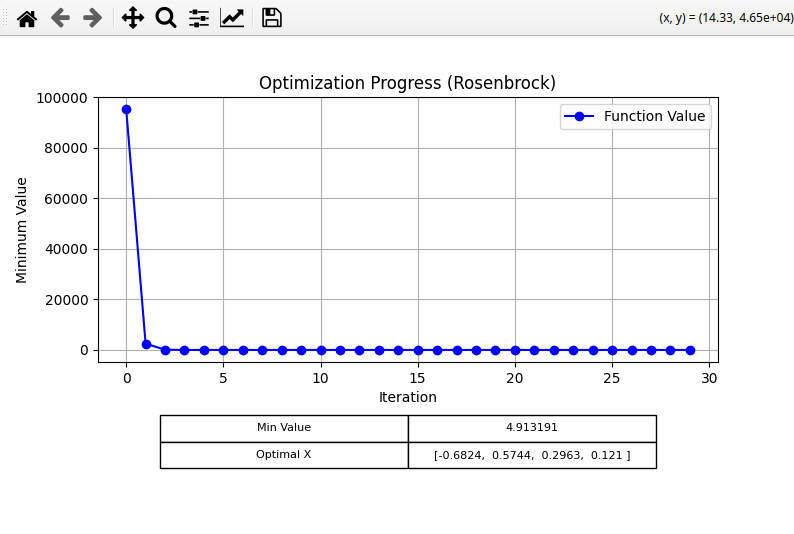
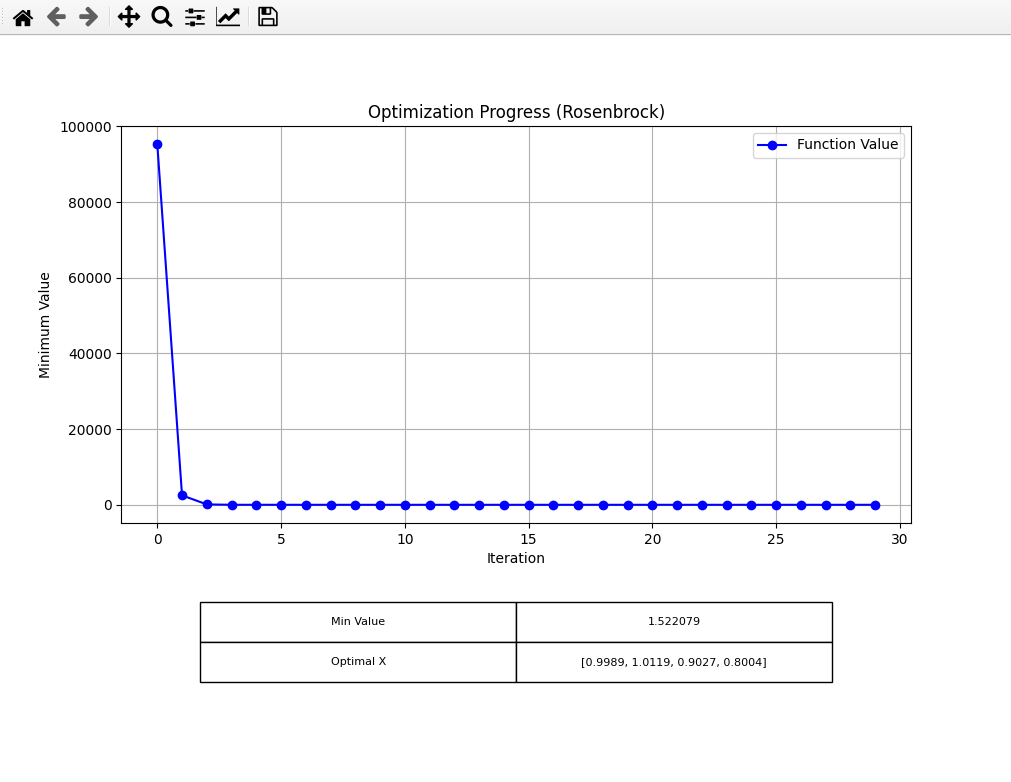
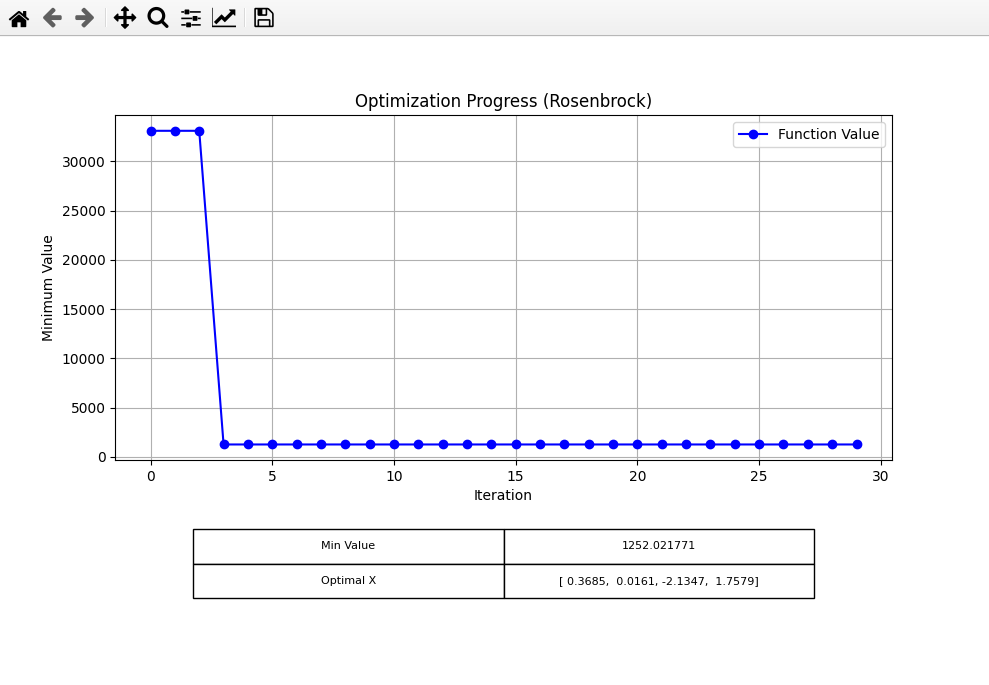
Rosenbrock
Next, I tried the Rosenbrock function, with the following settings:
For LS, I got:
For SHC, I got:
Further experimenting with Rosenbrock
I also tried adjusting some of the settings with the Rosenbrock function, to compare how they affect the LS and SHC algorithms. Each time, I only modified a single settings, with the rest matching the original Rosenbrock configuration (already shown above).
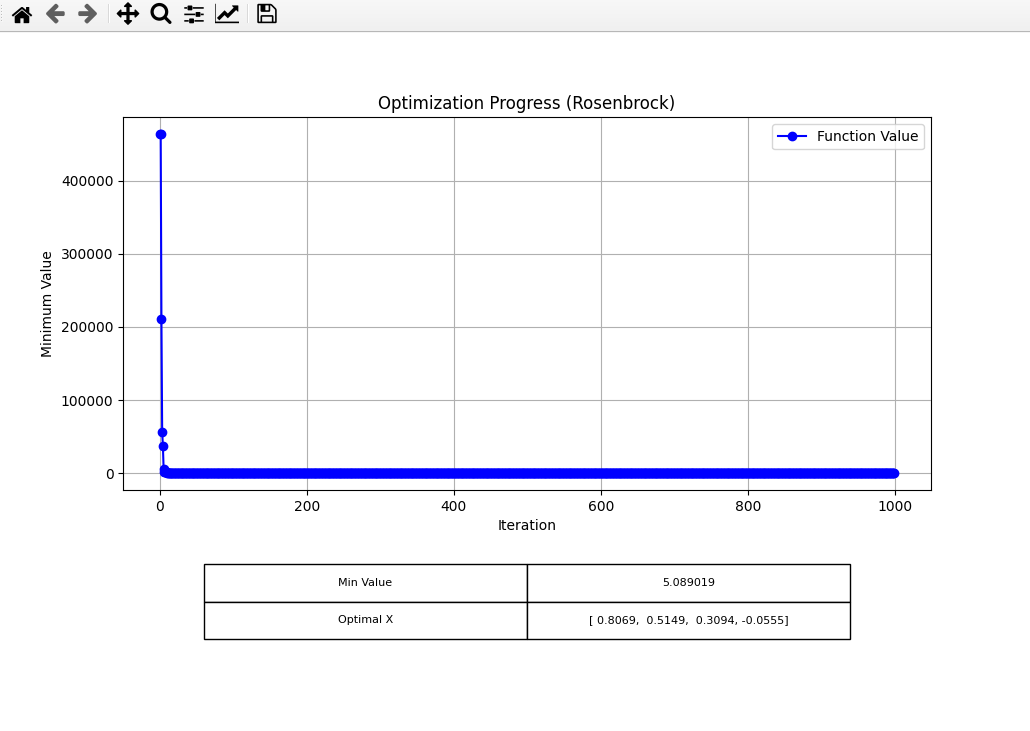
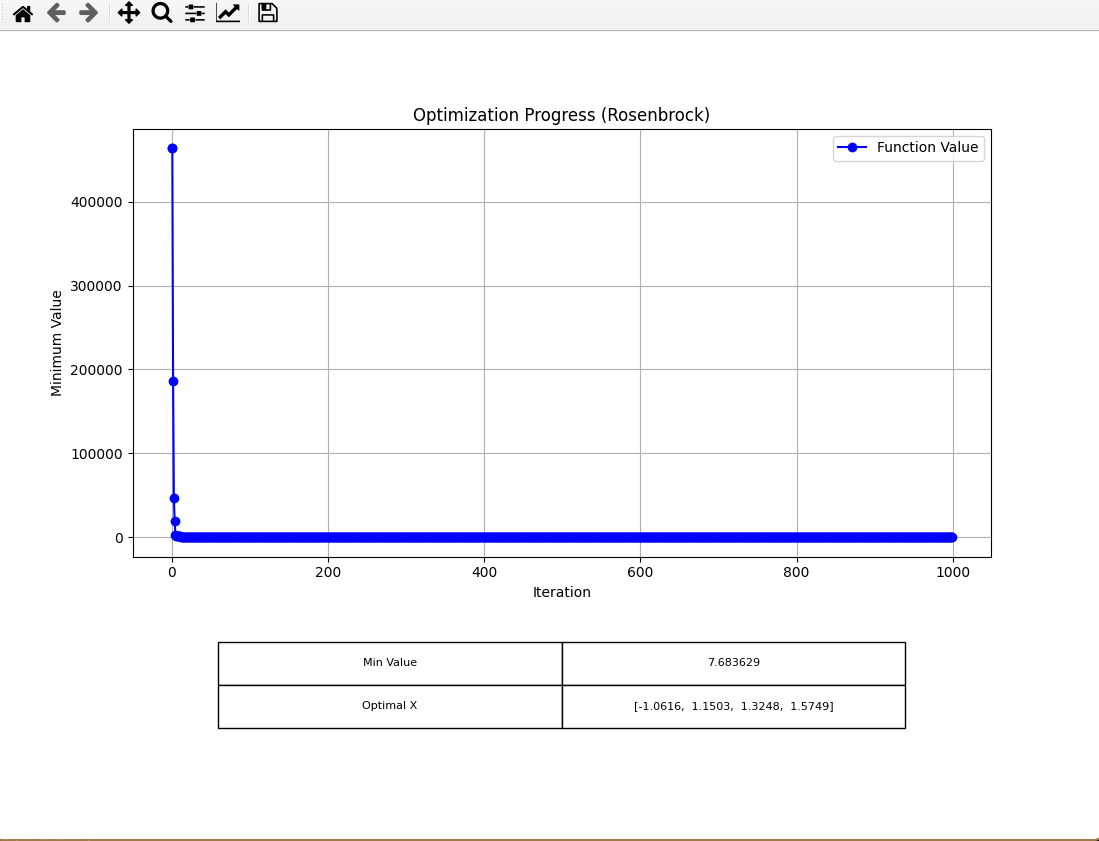
1000 iterations
I first tried increasing the number of iterations to 1000 (from 30).
For LS, I got:
for SHC, I got:
100 neighbors
I then tried increasing the amount of neighbor points to 100 (from 3).
For LS, I got:
for SHC, I got:
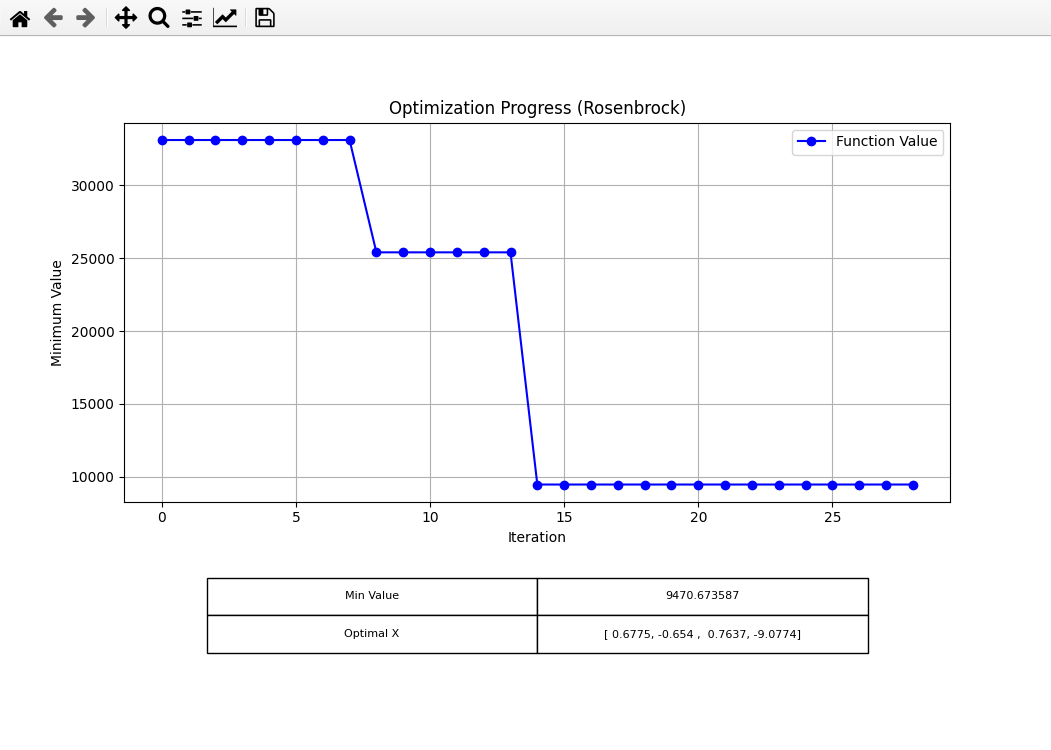
Standard deviation of 30
Finally, I tried increasing the standard deviation of the normal distribution to 30 (from 1.5).
For LS, I got:
for SHC, I got: